While getting some deep learning research practice, I decided to do some archaeology by reproducing some older deep learning papers.
Then, I recalled (back in my fast.ai course days) Jeremy Howard discussing U-Net and the impression it had on me—possibly the first time I encountered skip connections.
So I read the paper and wondered: Is it possible to reproduce their results only from the paper, and perhaps even critically examine some of the claims they make?
The full code is available on GitHub if you’re curious, but I thought it would be better to walk you through my adventure. Let's go!
Background
U-Net: Convolutional Networks for Biomedical Image Segmentation came out in 2015. Although they released their code (which uses the Caffe deep learning framework), I did not look at it on purpose. It’s not because I can’t read C++ to save my life; it’s part of the challenge—reproduce U-Net only from the paper. Let’s use our own eyes to read the words and look at the pretty pictures!
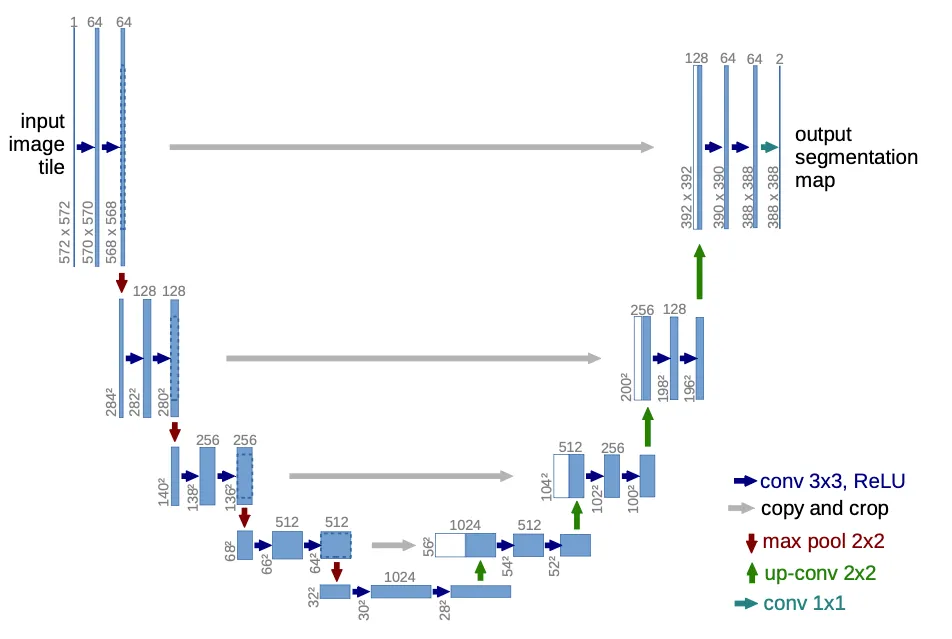
As the title of the paper suggests, U-Net uses convolutional networks to perform image segmentation, which means it takes an image as input with things in it and tries to predict a mask that differentiates the things from the background (or from each other, if it is multi-class).
It first puts an input image through a contraction path, where resolution decreases but channels increase, and then back up through an expansion path, where the opposite happens, ending up with a reasonably large image (but smaller than the input! more on that below) and a single channel (black and white).
A first look at the data
Here is a sample from the first dataset (which we call EM, for electron microscopy). It represents a cross-section of cells, and the mask differentiates cell bodies (white) from their membranes (black).
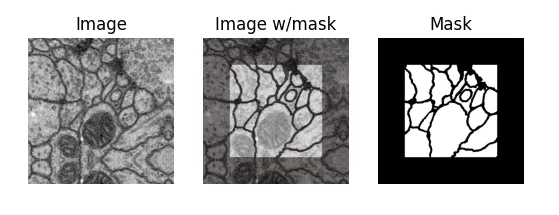
But why is the mask cropped, you may ask? Because of how convolutions move over an input image, even though their receptive field (what they see) is the entire input image, the output feature maps are a bit smaller (unless you use padding).
After many down and up-convolutions, the network's output will be smaller than the input, so our dataset must account for that: for an input image of 512x512, we can only predict a 324x324 output mask, which is necessarily a center-cropped version of the original full-size mask in the dataset.
The way I found out about this was the hard way, of course. When I first saw the EM dataset, which consists of input images and output masks all of 512x512 px, I naively tried to just resize down the output mask to fit the network's output, and it did not learn at all.
Looking around, I saw some people suggested padding the expansion path with zeros to make the residual connections fit (more on that later), which seemed to work. However, the paper mentioned none of that padding, so I thought something was off.
The penny dropped when the paper mentioned their overlap-tiling strategy. To process arbitrarily large images regardless of GPU VRAM, we must process images one fixed-size tile at a time.
And if for any input tile we can only predict a center-cropped mask, we won’t learn to predict the masks in the corners! What a waste of good, valuable data. To solve that, our dataloader just needs to select a random output mask tile (even if it’s at the top left corner) and then make up the original input image that would predict that tile. If the mask tile was in some corner, we’ll just make up the surrounding context by reflecting the original image. A bit hand-wavy, but hey, that’s deep learning for you!
Even though the architecture image is pretty self-explanatory, I found a couple of caveats worth mentioning:
It assumes an input of 572x572 px, which I used to sanity-check the feature map sizes after every convolutional layer and pooling operation. The EM dataset’s input is 512x512 px, however.
The paper mentions a dropout layer "at the end of the contraction path," though it is not pictured. I decided to put it right before the first up-convolution, but it is unclear where they actually put it.
Model Implementation
Here is the model code:
import math
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision.transforms.functional import center_crop
class Conv(nn.Module):
def __init__(self, in_channels, out_channels):
super().__init__()
self.conv = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=(3, 3)),
nn.ReLU(inplace=True),
nn.Conv2d(out_channels, out_channels, kernel_size=(3, 3)),
nn.ReLU(inplace=True),
)
def forward(self, x):
return self.conv(x)
class Model(nn.Module):
def __init__(self, n_classes, dropout=0.0):
super().__init__()
self.contraction = nn.ModuleList(
[
Conv(1, 64),
Conv(64, 128),
Conv(128, 256),
Conv(256, 512),
Conv(512, 1024),
]
)
self.dropout = nn.Dropout(p=dropout)
self.up_convs = nn.ModuleList(
[
nn.ConvTranspose2d(1024, 512, kernel_size=(2, 2), stride=2),
nn.ConvTranspose2d(512, 256, kernel_size=(2, 2), stride=2),
nn.ConvTranspose2d(256, 128, kernel_size=(2, 2), stride=2),
nn.ConvTranspose2d(128, 64, kernel_size=(2, 2), stride=2),
]
)
self.expansion = nn.ModuleList(
[
Conv(1024, 512),
Conv(512, 256),
Conv(256, 128),
Conv(128, 64),
]
)
self.max_pool = nn.MaxPool2d(kernel_size=(2, 2), stride=2)
self.out_conv = nn.Conv2d(64, n_classes, kernel_size=(1, 1))
# Initializations as per the paper
for mod in self.modules():
if isinstance(mod, nn.Conv2d) or isinstance(mod, nn.ConvTranspose2d):
n = mod.kernel_size[0] * mod.kernel_size[1] * mod.in_channels
nn.init.normal_(mod.weight, mean=0, std=math.sqrt(2.0 / n))
def forward(self, x):
residuals = []
for idx, contraction in enumerate(self.contraction):
x = contraction(x)
if idx < len(self.contraction) - 1:
residuals.insert(0, x) # residuals will be reversed
x = self.max_pool(x)
x = self.dropout(x)
for idx, (up_conv, expansion) in enumerate(zip(self.up_convs, self.expansion)):
x = up_conv(x)
residual = center_crop(residuals[idx], (x.shape[-2], x.shape[-1]))
x = torch.concat(
[residual, x], dim=1
) # concat the residual along the channel axis
x = expansion(x)
return self.out_conv(x)Let’s look at the forward pass in detail. The contraction path is a series of Conv layers (each with two 3x3 Conv2Ds and ReLU activations) with max pooling in-between, which halves the resolution.
As we go down the contraction path, notice that we save the Conv activations (before max pooling) in a residuals list. As per the architecture diagram, we will need to concatenate those in parallel to their counterparts in the expansion path. Again, since the counterparts will be of smaller resolution, the residuals will need to be center-cropped.
At the end of the contraction path, we do a dropout and go back up through the expansion path, concatenating the contracted channels with the expanded ones. This concatenation effectively provides a high-bandwidth residual connection for the gradients to flow back.
Finally, an output convolution gets the final predicted mask with a single channel (black and white).
Loss Function
The loss function is cross-entropy (or equivalently log-softmax plus negative log-likelihood), but there is a twist.
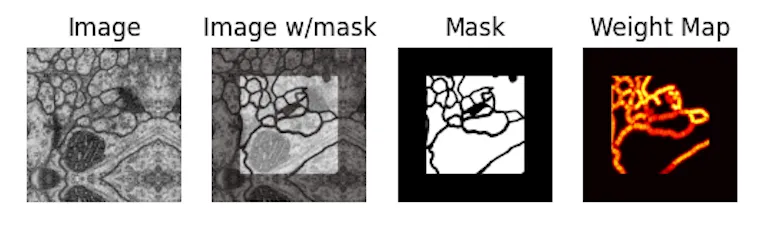
On the EM dataset, they introduced a weighted loss with a synthesized weight map that uses morphological operations on the original mask to highlight the borders between cells:
def criterion(pred, targets, weight_maps):
loss_per_pixel = F.nll_loss(pred, targets, reduction="none")
weighted_loss = loss_per_pixel * weight_maps
return weighted_loss.mean()This way, the loss is higher around cell borders, forcing the network to work harder to get those right.
Coming from the Holy Church of Gradient Descent, this looks like a cursed hack, so I added it to my list of assumptions/claims to verify.
Training Regime
For training, they use Stochastic Gradient Descent with a momentum of 0.99, though they do not mention a learning rate (I set it at 1e-03). I wondered, "Why not Adam?" so another one for the bag of things to verify.
Their set tile size was 512, which is essentially no tiling.
Data Augmentation
Since the datasets are very small (30 training images in the EM dataset!), the authors of the paper rightly put a lot of effort into data augmentation, settling on a combination of:
Tiling: for a given image, as long as the tiles are smaller than the image, there are several tiles. The authors do claim, though, that to maximize GPU utilization, they favor larger tiles over larger batch sizes. At face value this makes sense from a GPU utilization standpoint, but because I was not sure how it might affect the final loss, that goes into my bag of claims to verify.
Elastic Deformations: This one is fun! They warp the images with realistic deformations you might see in cells, providing more variety so the network does not overfit to the same-shaped cells.
Dropout at the end of the contraction path: just to be sure.
It is important to note that those 30 training images are very highly correlated, too, since they are consecutive slices within one single 3D volume. So it makes sense to deploy every data augmentation trick in the book.
Expected results
So, to reproduce the paper, what results are we matching? The authors trained their architecture for three segmentation challenges:
1. EM Segmentation Challenge 2015 (with the EM dataset, generously uploaded to GitHub by Hoang Pham). They are evaluated on Warping Error (0.000353), Rand Error (0.0382), and Pixel Error (0.0611), defined in the paper.
2. ISBI cell tracking challenge 2015 (PhC-U373 dataset, available here): they achieved an Intersection Over Union (IoU) of 0.9203.
3. ISBI cell tracking challenge 2015 (DIC-HeLa dataset, available here): they achieve an Intersection Over Union (IOU) of 0.7756.
As it turns out, the test sets for these are publicly available, but the test labels are not. One is supposed to send the predicted probability maps to the organizers and get back an evaluation result. Unfortunately, ain't nobody got time for that (probably least of all the organizers), so we’ll have to take the authors’ word for it.
To make sense of anything, we will have to settle on a lesser metric: loss on a validation set, which we will set at 20% of the training set. As I’ve mentioned, the datasets are highly correlated, so leakage is guaranteed, but it is literally the best we can do with what we have, short of hand-labeling the test set myself.
Experiments
All experiments are trained for 4K update steps, with batch size 4 and 512x512 tiles (so, 1M pixels seen per update), on 80% of the training set. We report training loss, validation loss, and IOU on the validation set. We also torch.compile the model for extra speed.
After running the baselines, I dump the bag of things to verify, and the questions that interest me are:
Authors claim that larger tiles are better than larger batch sizes. How do tile size versus batch size compare, keeping pixels seen constant?
[For the EM dataset only] Weight maps seem like an awkward inductive bias. Do they help?
Would Adam work better than SGD here?
Datasets
We already introduced the EM dataset with the synthetic weight maps:

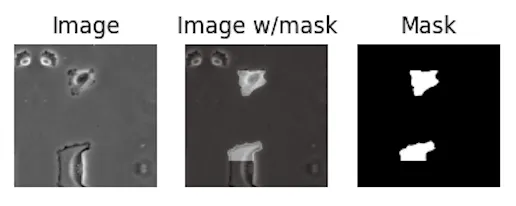
For reference, the other two datasets are PhC-U373 (you can see the reflected bottom part in this one):
And DIC-HeLa:

Baselines
First, I wanted to set a baseline for each of the three datasets as close as possible to what the authors did.
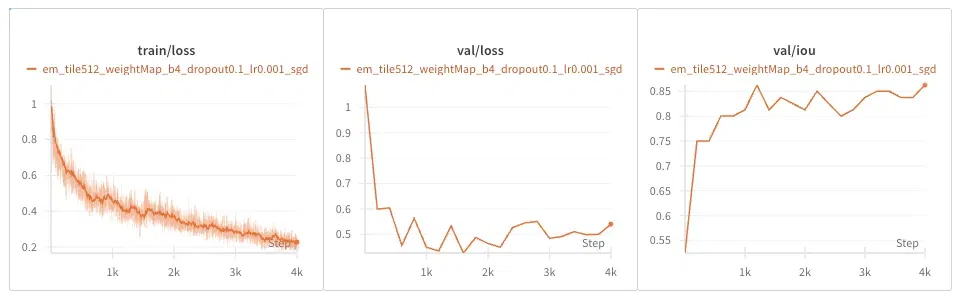
EM Dataset
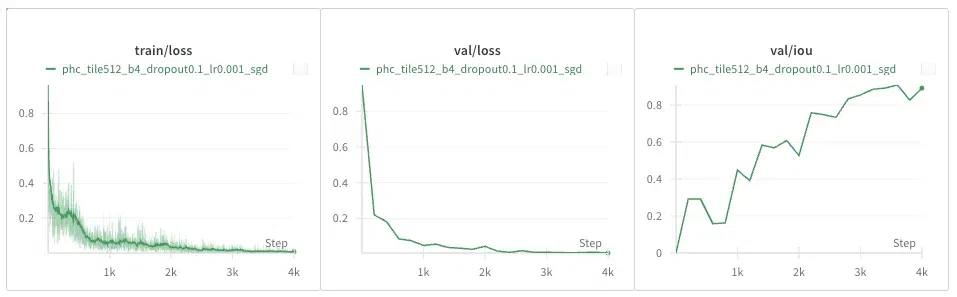
PhC-U373 Dataset
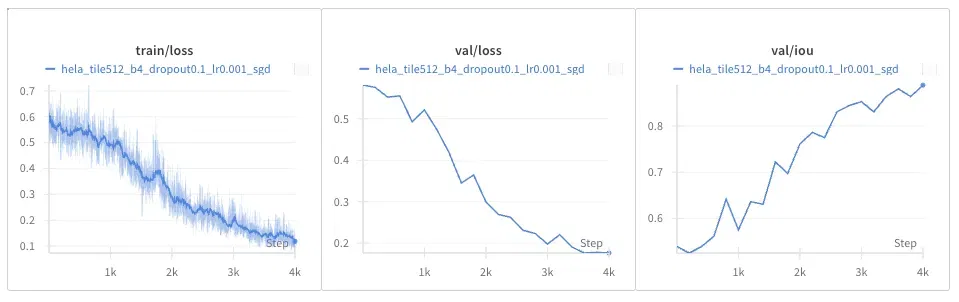
DIC-HeLa Dataset
Question #1: Larger tiles or larger batch size?
Fixing pixels seen per update at 1M, let's compare batch size 4 with 512x512 tiles against batch size 16 with 256x256 tiles.
EM Dataset

As expected, training is noisier with smaller tiles, as are validation loss and IOU.
PhC-U373 Dataset
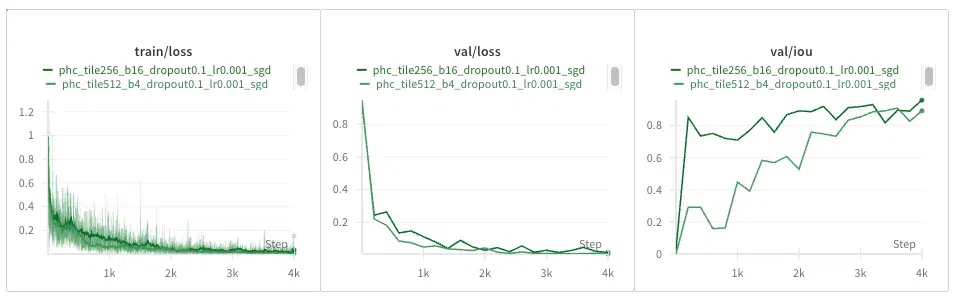
Interestingly, smaller tiles seem a bit noisier and converge slower loss-wise, but the IOU seems higher. Could it be, though, that if masks are sparser in this dataset, more tiles are blank, causing the IOU to look artificially better earlier?
DIC-HeLa Dataset
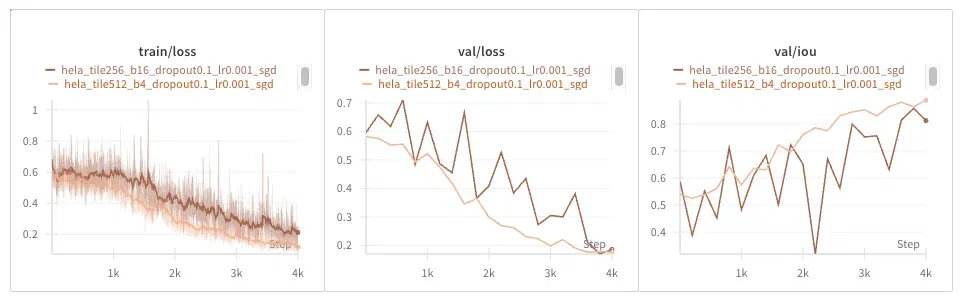
The same result occurs as with the EM dataset: everything is noisier.
Conclusions and thoughts
Why is everything noisier? We need to keep in mind that the input tiles are 256x256, but the output masks end up being only 68x68 pixels. The final loss is the average of each individual pixel’s loss, so you might think at first that fewer pixels result in a noisier loss. But we compensate with a larger batch size, so in the end each update averages 1M pixel losses, no matter the setting.
Does this tell us there is more variation across samples in our dataset than across tiles?
I conclude that larger tiles are better, just like the authors claim, but I’m still not sure why they lead to smoother training dynamics.
Question #2: Do synthetic Weight Maps in the EM dataset really help?
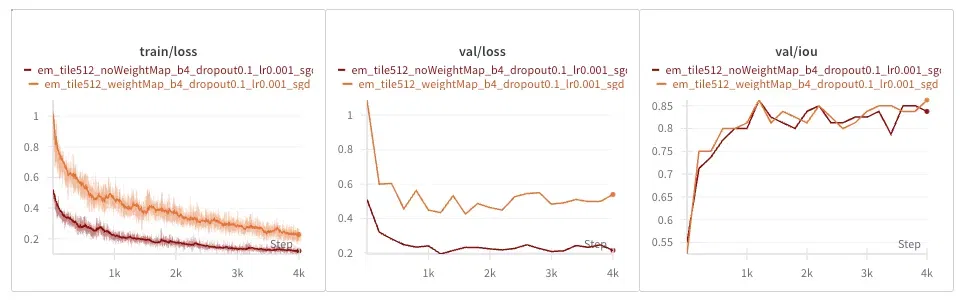
Train and validation loss look lower without weight maps, but the reason is that the loss function is different! The weight-map weighted loss is necessarily higher because we are scaling up border-adjacent pixel losses.
However, the IOU metric tells a clearer story: there is no noticeable difference between having and not having this weighted loss.
The weight maps turn out to be just a hacky inductive bias. My faith in the Holy Church of Gradient Descent remains intact, for now.
Question #3: Would Adam converge faster than SGD?
EM Dataset
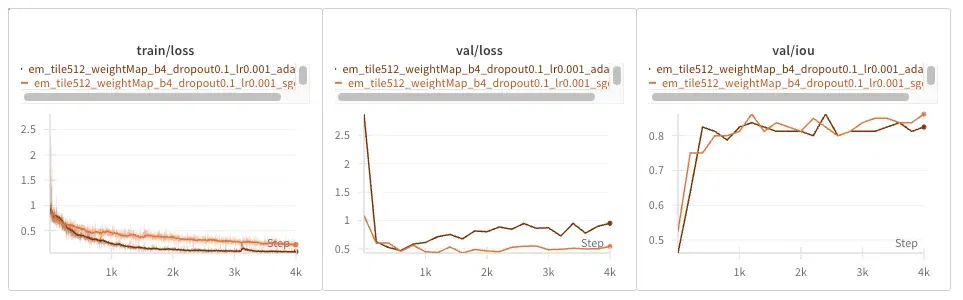
Adam converges faster in training loss but seems to overfit faster, producing seemingly diverging validation loss. IOU seems unaffected.
PhC-U373 Dataset
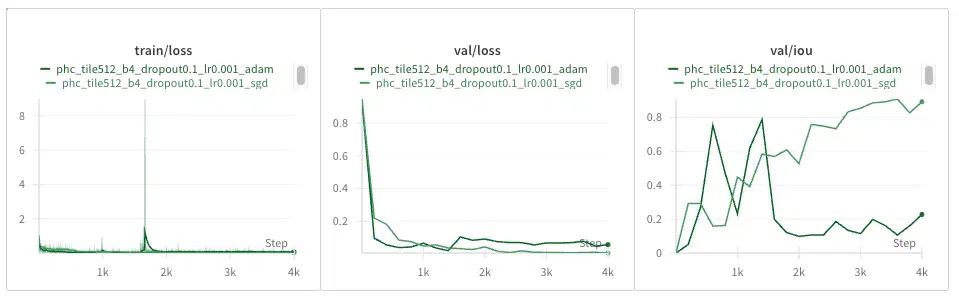
Adam really drops the ball here, with a massive loss spike and learning who knows what, by the looks of the IOU completely diverging.
Let us reduce the learning rate from 1e-03 to 3e-04:

Much better, though a loss spike remains in the same spot. It recovers quickly and achieves the best IOU from 2K steps onwards!
DIC-HeLa Dataset
We need to bring down the learning rate again from 1e-3 to 3e-4.

Much nicer! Loss and IOU converge much faster too.
Conclusions / thoughts
Adam converges faster with a lower learning rate.
Let us re-run the EM dataset with the lower learning rate, for good measure:
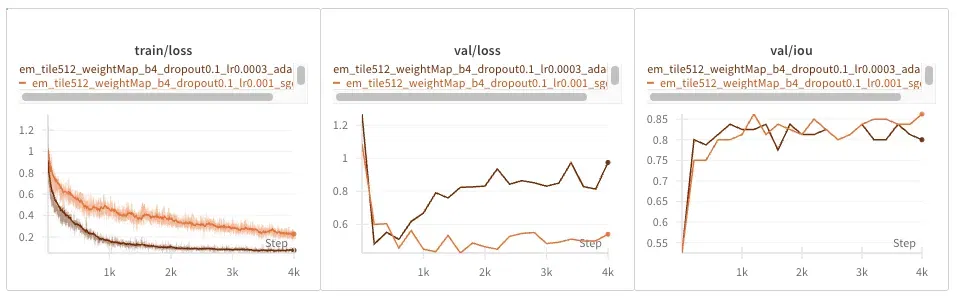
The EM dataset is much smaller, so it seems to similarly overfit; that is perhaps not surprising.
Conclusion
I had fun doing this, and I experienced firsthand the reproducibility crisis in deep learning.
If you are interested in getting better at this and exercising your critical thinking skills, I recommend you try this too.
It is especially exciting when it comes to older papers because they can be more obscure, leaving more to figure out yourself, and at the same time they are easier to reproduce on today's consumer hardware.
And if you are interested in reading about my next adventure reproducing older papers, watch this space!